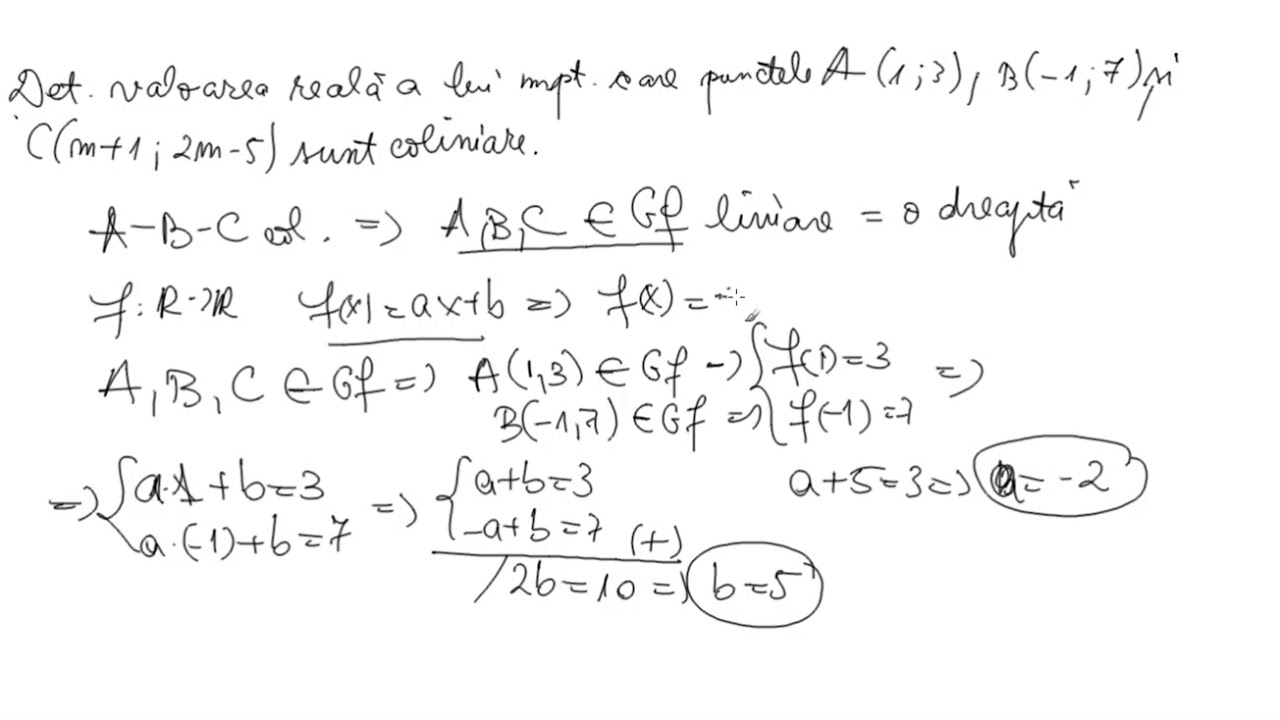Cand 2 Vectori Sunt Coliniari

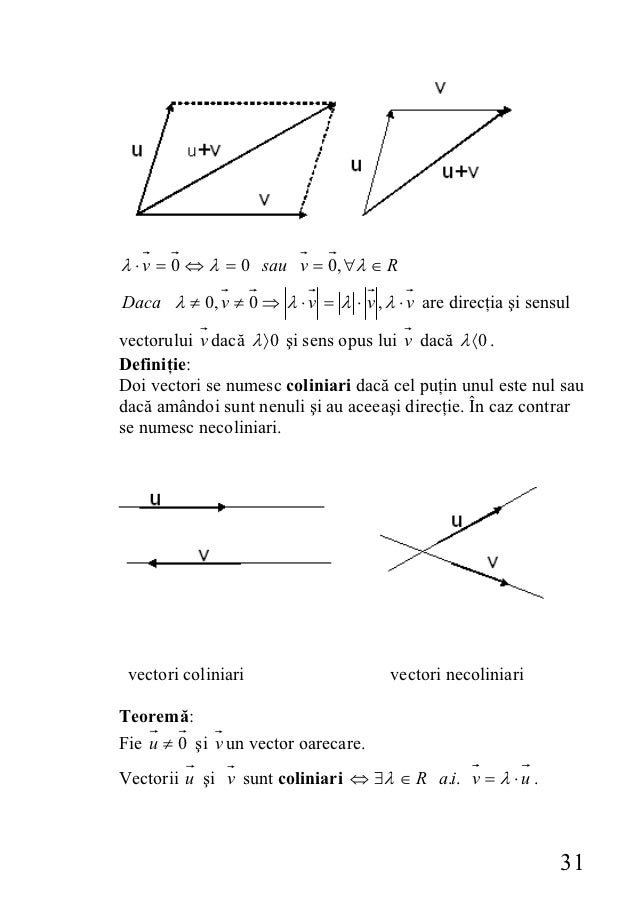
Definitia 2 1 5 daca asi bsunt doi vectori având reprezentan tii.

Cand 2 vectori sunt coliniari. Când ambii vectori sunt nenuli și dreptele lor suport sunt paralele sau coincid. Lun ian 09 2012 4 19 pm. Mesaj de mrsilent47 mar ian. Atunci vectorul sumă va avea aceeași direcție și același sens cu vectorii și iar modulul sau lungimea lui va fi suma modulelor celorlalți doi.

Este o formula cand vectorii sunt coliniari si anume x1 x2 y1 y2 si inlocuiesti ca u si v sa fie paraleli trebue sa fie egale urmatoarele rapoarte. Mesaj de ex admin mar ian 10 2012 7 39 pm stii conditia de coliniaritate a doi vectori. în primul rând să luăm vectorii respectiv ca având același sens. Așadar 2 vectori sunt coliniari dacă au coeficienții proporționali.

V 1 este coliniar cu v 2 dacă x 1 x 2 y 1 y 2 v 1 perpendicular. Jitaruionelblog pregatire bac si evaluarea nationala 2021 la matematica si alte materii. Materiale lectii formule exercitii rezolvate matematica gimnaziu si liceu. Exemple scrise de profesor jitaru ionel.

Sunt doar niște notații generale. Cand a b c sunt colineare si vectorii ab si bc au acelasi sens atunci u v u v. Dacă u ai bj și într un exercițiu ai u 2i 3j atunci a 2 și b 3. 2 8 3 12 1 4 u v si.

Produsul scalar a doi vectori. Articole din condiția de coliniaritate doi vectori sunt coliniari dacă și numai dacă au coeficienții proporționali. Dacă v ci dj și într un exercițiu ai v 4i 8j atunci c 4 și d 8. Am notat cu u și v 2 vectori.

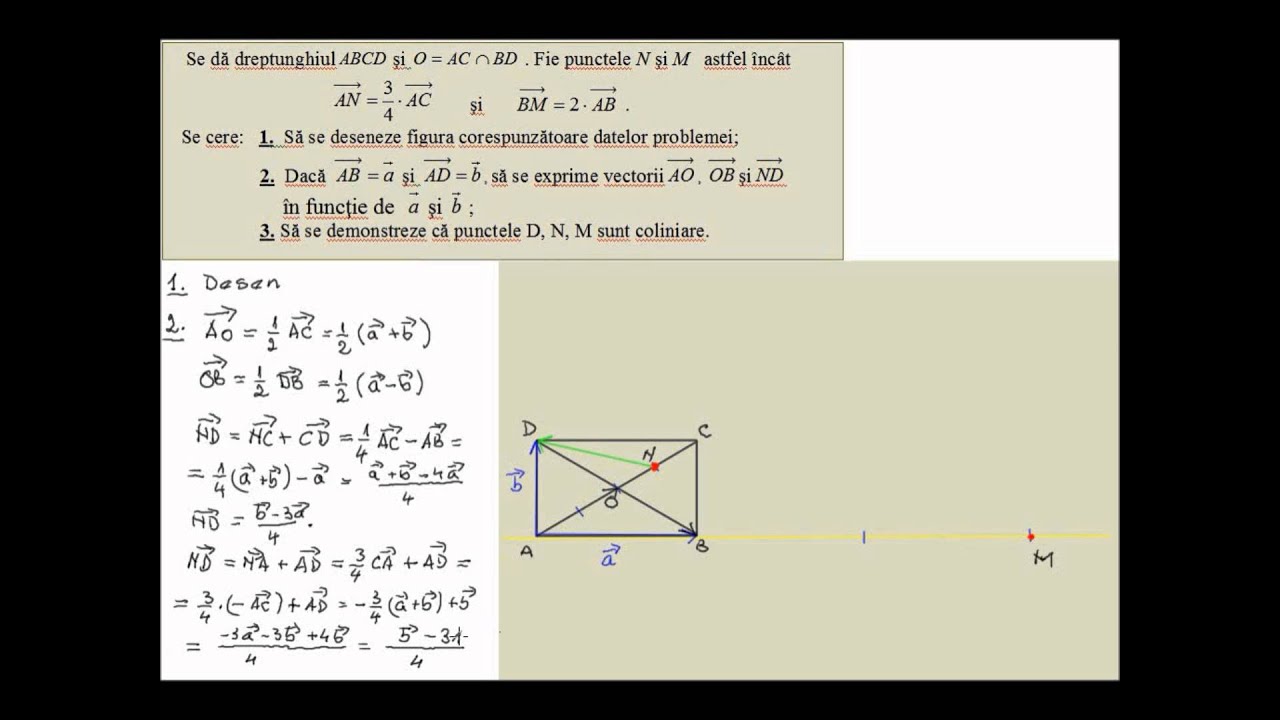
Determinati numărul a 0 pentru care vectorii v1 si v2 sunt coliniari. Daca u x1 a y1 b si v x2 a y2 b si a si b vectori atunci trebue ca. V 1 v 2 x 1 x 2 y 1 y 2 v 1 v 2 v 1 v 2 c o s v 1 v 2 modulul lungimea unui vector u a i b j este u a 2 b 2. Vectori coliniari doi vectori se numesc coliniari dacă au aceeași direcție.

M 5 7 3m sunt perpendiculari daca. Sunt doi vect u si v u mi 7j v 5i 3mj paraleli sau coliniari sunt daca. Dacă vectori sunt coliniari atunci ei au aceeași direcție. Mie ian 24 2007 10 29 pm.

Vectorii respectivi pot fi notați cu orice litere. Teorema 2 1 6 daca vectorii v v1 v2 sunt coplanari si vectorii v1 si v2 nu sunt coliniari vezi remarca 2 1 8 atunci existaînmodunicdoiscalari. Deci in general u v u v pentru orice 2 vectori u si v egalitatea avand loc numai daca u si v sunt coliniari si au acelasi sens. Acest lucru se întâmplă în doua cazuri.